赌徒只想永远沉浸在自己设定的幻境之中,而这种制造幻境的驱动力被引向了另一个方向,这个方向的归宿就是倾家荡产。
10月4日,币圈“世纪审判”拉开帷幕,犯下“美国史上最大金融诈骗案之一”的昔日币圈大佬Sam Bankman-Fried(SBF)迎来了决定他命运的最终审判。
就在SBF出庭的第一天,10月3日,《大空头》的作者,著名商业作家Michael Lewis关于SBF的新书《Going Infinite:The Rise and Fall of a New Tycoon》(《走向无限》)也正式上市。

在这本书中,Lewis采访了曾与SBF有过接触的同学、同事以及亲友,在听闻SBF的事迹之时,Lewis意识到,赌徒心理早已根植于SBF的内心,从顶级富豪到资产一夜清零的结局或许早已注定。
Jane Street的实习期赌局
书中描述了这样一件事,SBF曾经的老东家Jane Street希望能在交易员们的实习期教会他们如何下注思考,因此鼓励实习生互相对赌,赌的内容可以是他任何他们能想到的东西——哪支球队会赢?哪些实习生会获得全职工作机会?等等,但为了防止灾难发生,有一条规定——实习生一天的损失不能超过100美元。
一天清晨,书中称为“Asher Mellman”的实习生提出要与SBF打赌,赌的内容就是实习生当天损失的最大金额。
双方以65美元为打赌金额:如果任何实习生当天损失超过 65 美元,Asher将向SBF支付该实习生超过65美元的损失;如果没有人损失超过65美元,那么SBF将向Asher支付65美元与最大损失之间的差额。
也就是说,如果实习生损失达到了100美元,SBF将得到35美元,而如果实习生最多损失50美元,SBF则会向Asher支付15美元。
当然有一种情况,SBF可以选择自己输掉 100 美元,这样就可以轻松赢得这场赌局,但这对他来说这并不是最佳选择,作为有赌徒天性的SBF进行了一场在他自己看了相当“聪明“的交易。
在和Asher定好赌局后,SBF立即向房间里的其他实习生喊道:谁想和我来一场赌注为98美元的掷硬币的赌局?谁愿意为了98美元和我一起掷硬币,我就给谁一美元!
书中写道,那时Jane street的实习生都沉迷于期望值为正的赌局,几位实习生响应了SBF:
掷硬币本身是一个五五开的命题,因此接受SBF赌局的人的期望值为1美元:(0.5 × 98 美元)-(0.5 × 98 美元)+ 1 美元 = 1 美元。
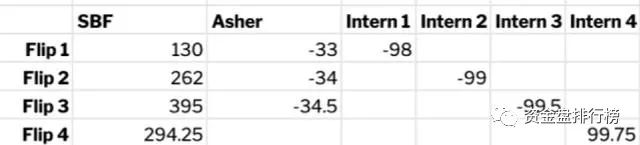
而SBF在这场赌局中的期望值更高,首先无论SBF的输赢, Asher必须向他支付 33 美元(98 美元-65 美元)。如果 SBF在掷硬币赌局中获胜,他将获得 98 美元(赢得抛硬币),再加上 33 美元(来自Asher),减去 1 美元(他向实习生支付了抛硬币的额外费用),净收益为 130 美元。
如果SBF输了,他会损失98美元(抛硬币)加上1美元(付款),但会拿回33美元(Asher给的),净损失为66美元。
书中分析称,这场赌局对SBF来说是期望值非常高:SBF有50/50的机会赢得130美元或仅损失66美元。在这场赌局,受伤的或许只有Asher,只有他的期望值为负,无论SBF和另一位实习生的赌局是什么情况,Asher都输了。
赌局开始了,在第一场价值98美元的赌局中,SBF成功押中了硬币的正反面,将赌注提高到 99 美元,并赢得第二次押注,他再次将赌注提高到了99.5美元,第三场赌局中,SBF还是赢了。第四场赌局中,SBF将赌注提高到 99.75 美元,然后他输了。
在Lewis的采访中,当时在Jane Street的实习生们都对SBF不顾Asher的感觉,一次又一次“羞辱”Asher感到厌恶。
但其实在这场赌局中,Asher并非全无胜算,当SBF问出,谁愿意和我展开一场值98美元的掷硬币赌局,我就给谁1美元时,Asher应该回答:我愿意,如果事情朝这样的方向发展,那一切发展都会不同。
虽然,此刻仍然是SBF的期望值更高,但Asher仍然有50/50的机会决定性地赢得赌局:
首先,参与赌局会给Asher带来更大风险的同时也会带来更多的回报:
– 如果他让别的实习生参与,他一定会损失≥33美元
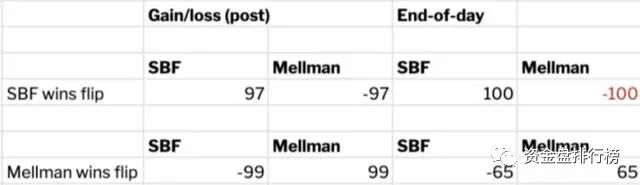
– 如果他参与,他要么损失100美元,要么赚66美元。
这似乎也限制了SBF的上涨空间。由于Asher的损失上限为100美元,因此如果损失97美元,他将无法支付赌注中的余额,这意味着SBF(大概)获利 100 美元,而不是 130 美元。
倾尽所有的赌徒
SBF曾口述了部分赌局的内容,他说:“当你用正确的表达勾起他人的兴趣时,人们会变得如此着迷于免费的美元。”
有评论指出,在这个故事以及其他关于SBF早期交易生涯的轶事中可以看到,SBF擅长计算期望值,善于找到方法来让交易对手感到痛苦,但他不擅长确定交易规模,且他根本就不考虑这个问题。
SBF对所有的交易都采取全力以赴的策略,在他的世界观中,如果你在赌局中存在1%的优势,你应该一次又一次地把你的所有钱都押上,直到你输光为止。
分析指出,作为Jane Street的实习生,你每天有100美元可以下注,你的部分工作就是用这100美元尽可能的多赚钱,但将全部资金(甚至98美元)投注在仅具有1%优势的单一投注上真的是最佳选择吗:
凯利公式指出,在一个期望收益为正的重复性赌局或者重复性投资中,每一期应该下注的最优比例。鉴于实习生的资金为 100 美元,我认为凯利会告诉你最多在这个赌注上投入10美元,98美元太多了。
当我读到这一段的时候,我会感叹Jane Street到底在教那些实习生什么?
但也有分析指出,回想一下2020年,SBF在X(原twitter)上与Matt Hollerbach关于凯利准则争论,SBF称,他的赌金肯定会比“凯利准则计算出的更多”。为什么呢?因为SBF更相信他的效用函数(衡量个人满足度的方式),不像传统模型中通常假定的是对数增长的,效用函数更接近于线性增长。
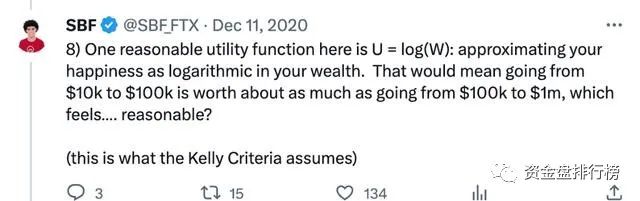
正因这样的心态,SBF更愿意“All in”,以追求更大的回报,因为他相信每一单位的额外收益对他的整体满足度有更大的影响,而不会担心风险。SBF告诉Lewis,他需要“无限资金
但或许正是“无限资金”背后被SBF忽视的”无限风险”最终将他推入深渊。
 一洼田
一洼田